Linear Case Study
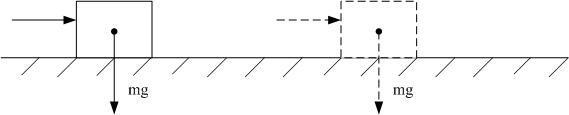
System model
 |
| Linear Case Study |
The system is a linear system. For a unit mass continuous time system,
it is
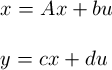
where x=[p v]', a=[0 1;0 0], b=[0 1]', c=[1 0], and d=0.
For a unit mass discrete-time system, it is
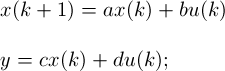
where x=[p v]', a=[1 T;0 1], b=[T^2/2 T]', c=[1 0], d=0. T is sample time, p is the position, and v is the velocity.
State-Feedback LQR (Linear Quadratic Regulation)
Synthesis:
The optimal state-feedback LQR is a simple matrix gain of the form
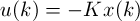 , where K is the gain matrix and is given by Algebraic Riccati Equation (ARE). (In Matlab, we can use "[K,S,e] = dlqr(a,b,Q,R)" to get K). When Q=[0.1 0;0 0] and R=1, we get K=[0.3100 0.7874]'.
, where K is the gain matrix and is given by Algebraic Riccati Equation (ARE). (In Matlab, we can use "[K,S,e] = dlqr(a,b,Q,R)" to get K). When Q=[0.1 0;0 0] and R=1, we get K=[0.3100 0.7874]'.
Result:
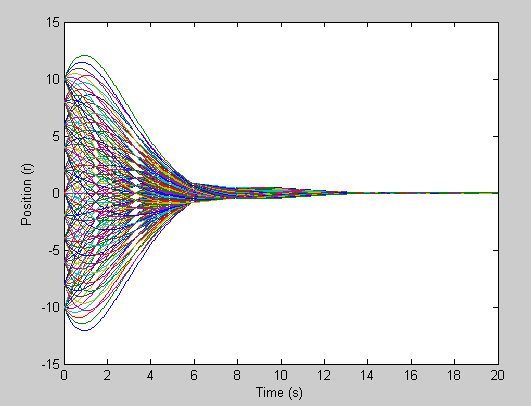 |
| Position |
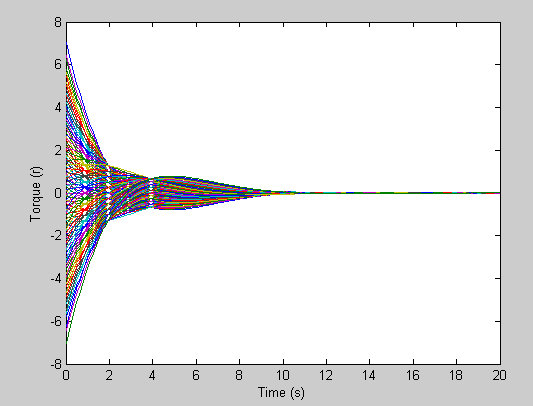 |
| Applied force for different initial state. |
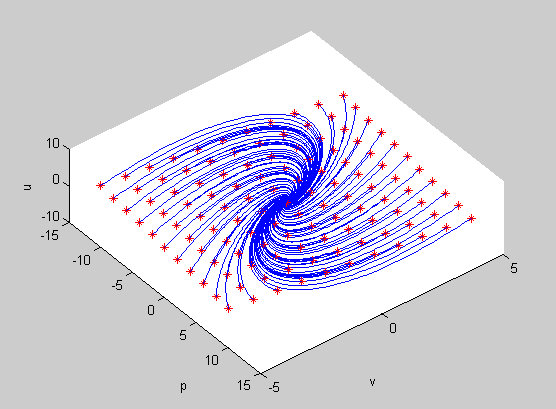 |
| Control policy. The trajectory (the blue lines) starts from the initial state (the red star) and terminates at the goal. |
Trajectory Optimization
This problem can also solve by the optimizer. In AMPL, this problem can be written as
param init_xp :=10;
param init_dxp :=0;
param pi := 4*atan(1);
param N := 500;
param time := 20;
param dt := time/N;
param mass := 1.0;
param goal := 0;
param state_penalty := 0.1;
var x{0..N} >= -15, <= goal + 15;
var v_offset{i in 0..N-1} = (x[i+1]-x[i])/dt;
var v{i in 1..N-1} = (v_offset[i]+v_offset[i-1])/2;
var a{i in 1..N-1} = (v_offset[i]-v_offset[i-1])/dt;
var u {i in 1..N-1} >=-5, <=5, :=0.0;
minimize energy:
sum {i in 1..N-1} (state_penalty*(x[i]-goal)*(x[i]-goal) + u[i]*u[i])*dt;
s.t. newton {i in 1..N-1}:
u[i] = mass* a[i];
s.t. x_init: x[0] = init_xp;
s.t. x_final: x[N] = goal;
s.t. v_init: v_offset[0] = init_dxp;
s.t. v_final: v_offset[N-1] = 0;
let {i in 0..N} x[i] := init_xp+(goal-init_xp)*i/N;
Results:
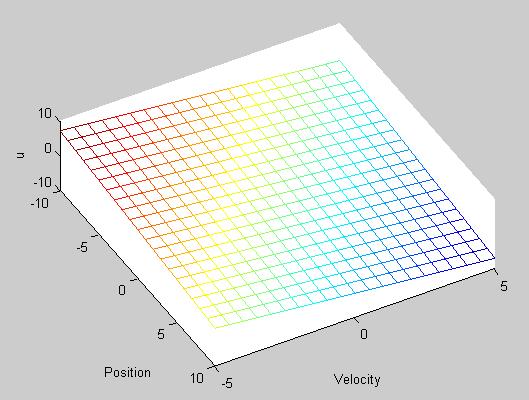 |
| Control policy |


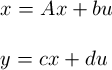
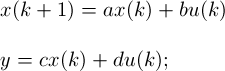
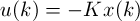 , where K is the gain matrix and is given by Algebraic Riccati Equation (ARE). (In Matlab, we can use "[K,S,e] = dlqr(a,b,Q,R)" to get K). When Q=[0.1 0;0 0] and R=1, we get K=[0.3100 0.7874]'.
, where K is the gain matrix and is given by Algebraic Riccati Equation (ARE). (In Matlab, we can use "[K,S,e] = dlqr(a,b,Q,R)" to get K). When Q=[0.1 0;0 0] and R=1, we get K=[0.3100 0.7874]'.



