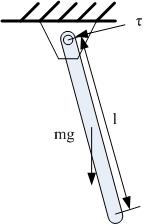
|
| One-link pendulum swing-up |
,
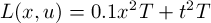where 0.1 weights the position error relative to the torque penalty, and T is the time step of the simulation (0.01s). There are no costs associated with the joint velocity.
Trajectory optimization in ampl. Code here
Trajectory optimization by Matlab.Code here
Controller indexed by time takes the form
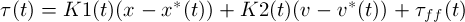
where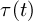 
is the driving torque, 
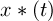and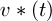 
is the optimal trajectory, and 
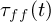is the feedforward optimal torque.
 |
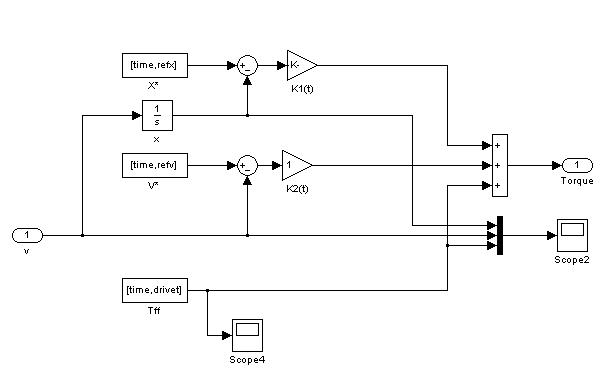| Controller's structure |
Dynamic simulation where p=0 and v=0
The controller takes the form
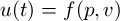
where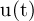 
is the driving torque, 
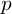and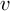 
the current position and velocity. In order to get optimal control policy, we generate optimal trajectories from a grid of starting points and use the first 
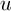as the optimal control for the state at the starting point.
Each trajectory is locally optimized using SNOPT.
Information is exchanged between trajectories to enable convergence to globally optimal
trajectories 1.
 |
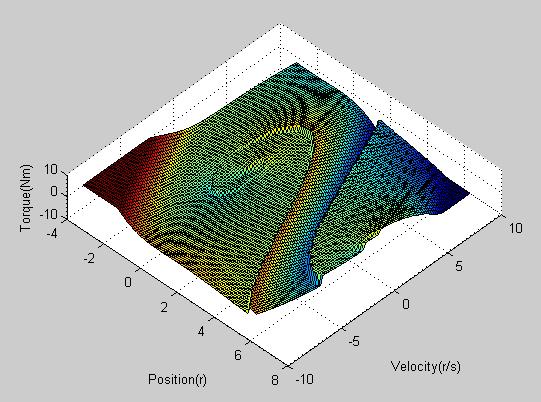| Optimal policy |
 |
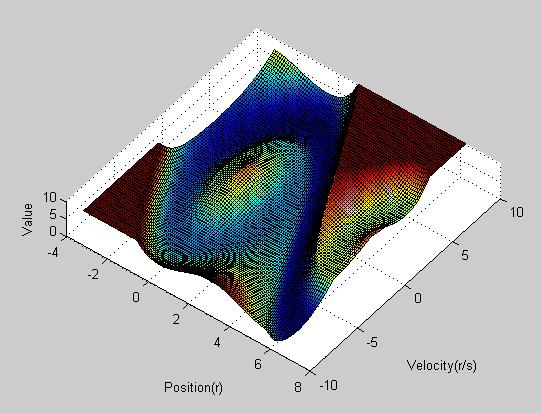| Value function |
 |
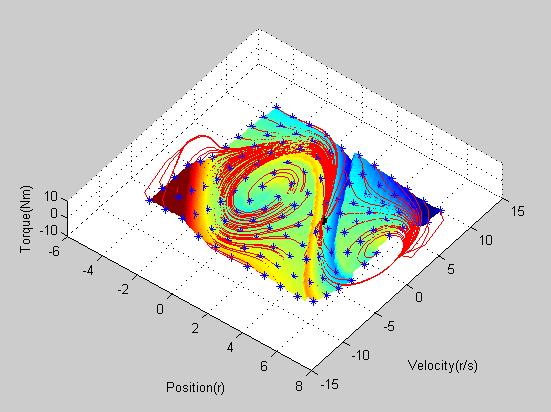| Optimal trajectory and policy |
1. Atkeson, C.G.; Stephens, B.J., "Random Sampling of States in Dynamic Programming," Systems, Man, and Cybernetics, Part B, IEEE Transactions on , vol.38, no.4, pp.924-929, Aug. 2008