Trajectory Optimization

Case study: a Linear System

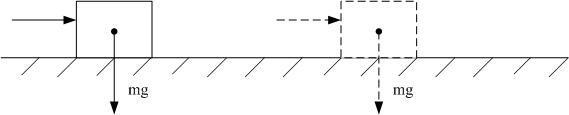
The optimal control for box pushing

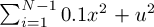In the first simple case, we apply a force on a box which is on the ground. We want to move the box to the original of the coordinate system in such a way as to minimize the total cost, $latex2png equation$ . Two different methods are used for this problem. See detail here

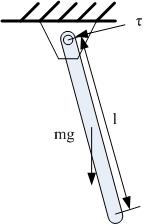Case study: One-link Pendulum Swing-up

One-link pendulum swing-up

In one link pendulum swing-up a motor at the base of the pendulum swings a rigid arm from the downward stable equilibrium to the upright unstable equilibrium and balances the arm there. What makes this challenging is that the one step cost function penalizes the amount of torque used and the deviation of the current position from the goal. The controller must try to minimize the total cost of the trajectory. 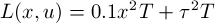The one step cost function for this example is a weighted sum of the squared position errors (difference between current angles and the goal angles) and the squared torques, $latex2png equation$ , where 0.1 weights the position error relative to the torque penalty, and T is the time step of the simulation (0.01s). There are no costs associated with the joint velocity. See detail here

Last Update: 2009-06-27-01:33:01

Home

Mail to me